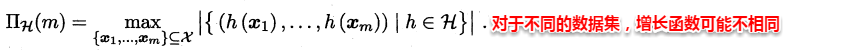• 13.3 VC维

    13.3 VC维

    现实中的学习任务通常都是无限假设空间，例如d维实数域空间中所有的超平面等，因此要对此种情形进行可学习研究，需要度量假设空间的复杂度。这便是VC维（Vapnik-Chervonenkis dimension）的来源。在介绍VC维之前，需要引入两个概念：

    增长函数：对于给定数据集D，假设空间中的每个假设都能对数据集的样本赋予标记，因此一个假设对应着一种打标结果，不同假设对D的打标结果可能是相同的，也可能是不同的。随着样本数量m的增大，假设空间对样本集D的打标结果也会增多，增长函数则表示假设空间对m个样本的数据集D打标的最大可能结果数，因此增长函数描述了假设空间的表示能力与复杂度。

    11.png

    打散：例如对二分类问题来说，m个样本最多有2^m个可能结果，每种可能结果称为一种“对分”，若假设空间能实现数据集D的所有对分，则称数据集能被该假设空间打散。

    因此尽管假设空间是无限的，但它对特定数据集打标的不同结果数是有限的，假设空间的VC维正是它能打散的最大数据集大小。通常这样来计算假设空间的VC维：若存在大小为d的数据集能被假设空间打散，但不存在任何大小为d+1的数据集能被假设空间打散，则其VC维为d。

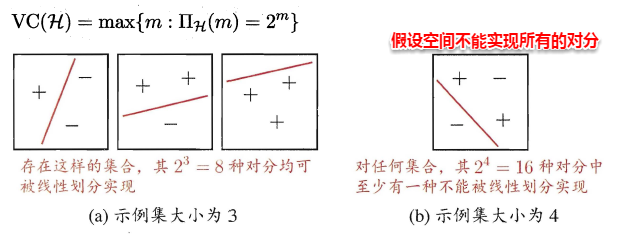
    12.png

    同时书中给出了假设空间VC维与增长函数的两个关系：

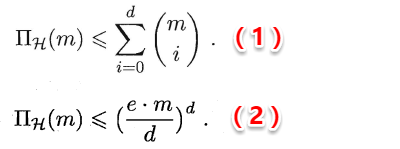
    13.png

    直观来理解（1）式也十分容易： 首先假设空间的VC维是d，说明当m<=d时，增长函数与2^m相等，例如：当m=d时，右边的组合数求和刚好等于2^d；而当m=d+1时，右边等于2^(d+1)-1，十分符合VC维的定义，同时也可以使用数学归纳法证明；（2）式则是由（1）式直接推导得出。

    在有限假设空间中，根据Hoeffding不等式便可以推导得出学习算法的泛化误差界；但在无限假设空间中，由于假设空间的大小无法计算，只能通过增长函数来描述其复杂度，因此无限假设空间中的泛化误差界需要引入增长函数。

    14.png

    15.png

    上式给出了基于VC维的泛化误差界，同时也可以计算出满足条件需要的样本数（样本复杂度）。若学习算法满足经验风险最小化原则（ERM），即学习算法的输出假设h在数据集D上的经验误差最小，可证明：任何VC维有限的假设空间都是（不可知）PAC可学习的，换而言之：若假设空间的最小泛化误差为0即目标概念包含在假设空间中，则是PAC可学习，若最小泛化误差不为0，则称为不可知PAC可学习。