7.2 极大似然法

极大似然估计（Maximum Likelihood Estimation，简称MLE），是一种根据数据采样来估计概率分布的经典方法。常用的策略是先假定总体具有某种确定的概率分布，再基于训练样本对概率分布的参数进行估计。运用到类条件概率p（x | c ）中，假设p（x | c ）服从一个参数为θ的分布，问题就变为根据已知的训练样本来估计θ。极大似然法的核心思想就是：估计出的参数使得已知样本出现的概率最大，即使得训练数据的似然最大。

所以，贝叶斯分类器的训练过程就是参数估计。总结最大似然法估计参数的过程，一般分为以下四个步骤：

* 1.写出似然函数；
* 2.对似然函数取对数，并整理；
* 3.求导数，令偏导数为0，得到似然方程组；
* 4.解似然方程组，得到所有参数即为所求。

例如：假设样本属性都是连续值，p（x | c ）服从一个多维高斯分布，则通过MLE计算出的参数刚好分别为：

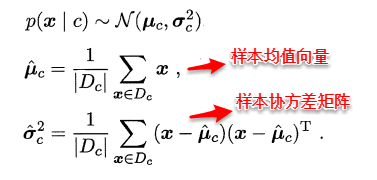
上述结果看起来十分合乎实际，但是采用最大似然法估计参数的效果很大程度上依赖于作出的假设是否合理，是否符合潜在的真实数据分布。这就需要大量的经验知识，搞统计越来越值钱也是这个道理，大牛们掐指一算比我们搬砖几天更有效果。