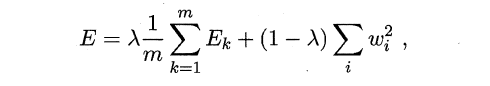5.3 BP神经网络算法

由上面可以得知：神经网络的学习主要蕴含在权重和阈值中，多层网络使用上面简单感知机的权重调整规则显然不够用了，BP神经网络算法即误差逆传播算法（error BackPropagation）正是为学习多层前馈神经网络而设计，BP神经网络算法是迄今为止最成功的的神经网络学习算法。

一般而言，只需包含一个足够多神经元的隐层，就能以任意精度逼近任意复杂度的连续函数[Hornik et al.,1989]，故下面以训练单隐层的前馈神经网络为例，介绍BP神经网络的算法思想。

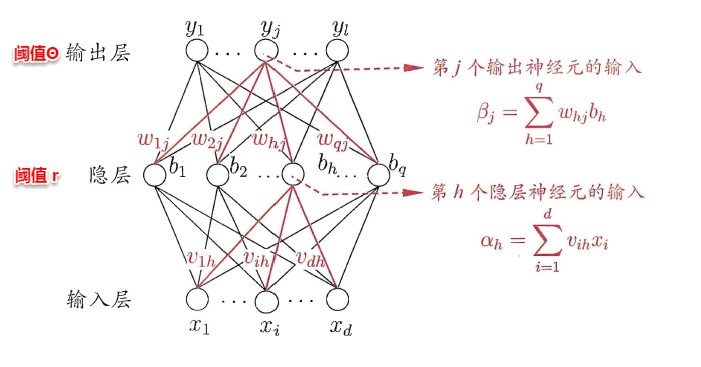
上图为一个单隐层前馈神经网络的拓扑结构，BP神经网络算法也使用梯度下降法（gradient descent），以单个样本的均方误差的负梯度方向对权重进行调节。可以看出：BP算法首先将误差反向传播给隐层神经元，调节隐层到输出层的连接权重与输出层神经元的阈值；接着根据隐含层神经元的均方误差，来调节输入层到隐含层的连接权值与隐含层神经元的阈值。BP算法基本的推导过程与感知机的推导过程原理是相同的，下面给出调整隐含层到输出层的权重调整规则的推导过程：

学习率η∈（0，1）控制着沿反梯度方向下降的步长，若步长太大则下降太快容易产生震荡，若步长太小则收敛速度太慢，一般地常把η设置为0.1，有时更新权重时会将输出层与隐含层设置为不同的学习率。BP算法的基本流程如下所示：

BP算法的更新规则是基于每个样本的预测值与真实类标的均方误差来进行权值调节，即BP算法每次更新只针对于单个样例。需要注意的是：BP算法的最终目标是要最小化整个训练集D上的累积误差，即：

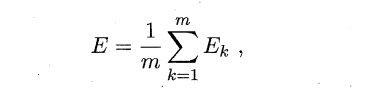
如果基于累积误差最小化的更新规则，则得到了累积误差逆传播算法（accumulated error backpropagation），即每次读取全部的数据集一遍，进行一轮学习，从而基于当前的累积误差进行权值调整，因此参数更新的频率相比标准BP算法低了很多，但在很多任务中，尤其是在数据量很大的时候，往往标准BP算法会获得较好的结果。另外对于如何设置隐层神经元个数的问题，至今仍然没有好的解决方案，常使用“试错法”进行调整。

前面提到，BP神经网络强大的学习能力常常容易造成过拟合问题，有以下两种策略来缓解BP网络的过拟合问题：

• 早停：将数据分为训练集与测试集，训练集用于学习，测试集用于评估性能，若在训练过程中，训练集的累积误差降低，而测试集的累积误差升高，则停止训练。
• 引入正则化（regularization）：基本思想是在累积误差函数中增加一个用于描述网络复杂度的部分，例如所有权值与阈值的平方和，其中λ∈（0,1）用于对累积经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计。