• 7.1 贝叶斯决策论

    7.1 贝叶斯决策论

    若将上述定义中样本空间的划分Bi看做为类标，A看做为一个新的样本，则很容易将条件概率理解为样本A是类别Bi的概率。在机器学习训练模型的过程中，往往我们都试图去优化一个风险函数，因此在概率框架下我们也可以为贝叶斯定义“条件风险”（conditional risk）。

    2.png

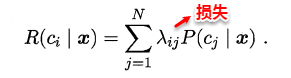
    我们的任务就是寻找一个判定准则最小化所有样本的条件风险总和，因此就有了贝叶斯判定准则（Bayes decision rule）:为最小化总体风险，只需在每个样本上选择那个使得条件风险最小的类标。

    3.png

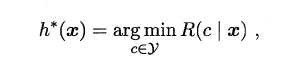
    若损失函数λ取0-1损失，则有：

    4.png

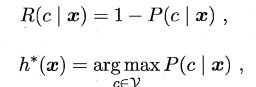
    即对于每个样本x，选择其后验概率P（c | x）最大所对应的类标，能使得总体风险函数最小，从而将原问题转化为估计后验概率P（c | x）。一般这里有两种策略来对后验概率进行估计：

    1. * 判别式模型：直接对 P（c | x）进行建模求解。例我们前面所介绍的决策树、神经网络、SVM都是属于判别式模型。
    2. * 生成式模型：通过先对联合分布P（x,c）建模，从而进一步求解 P（c | x）。

    贝叶斯分类器就属于生成式模型，基于贝叶斯公式对后验概率P（c | x） 进行一项神奇的变换，巴拉拉能量…. P（c | x）变身：

    5.png

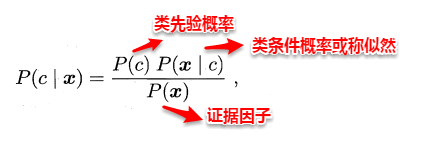
    对于给定的样本x，P（x）与类标无关，P（c）称为类先验概率，p（x | c ）称为类条件概率。这时估计后验概率P（c | x）就变成为估计类先验概率和类条件概率的问题。对于先验概率和后验概率，在看这章之前也是模糊了我好久，这里普及一下它们的基本概念。

    1. * 先验概率： 根据以往经验和分析得到的概率。
    2. * 后验概率：后验概率是基于新的信息，修正原来的先验概率后所获得的更接近实际情况的概率估计。

    实际上先验概率就是在没有任何结果出来的情况下估计的概率，而后验概率则是在有一定依据后的重新估计，直观意义上后验概率就是条件概率。下面直接上Wiki上的一个例子，简单粗暴快速完事…

    6.png

    回归正题，对于类先验概率P（c），p（c）就是样本空间中各类样本所占的比例，根据大数定理（当样本足够多时，频率趋于稳定等于其概率），这样当训练样本充足时，p(c)可以使用各类出现的频率来代替。因此只剩下类条件概率p（x | c ），它表达的意思是在类别c中出现x的概率，它涉及到属性的联合概率问题，若只有一个离散属性还好，当属性多时采用频率估计起来就十分困难，因此这里一般采用极大似然法进行估计。