选择排序

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

1. 算法步骤

1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置

2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

3. 重复第二步，直到所有元素均排序完毕。

2. 动图演示

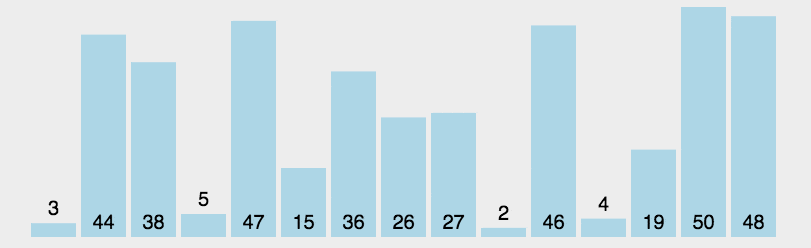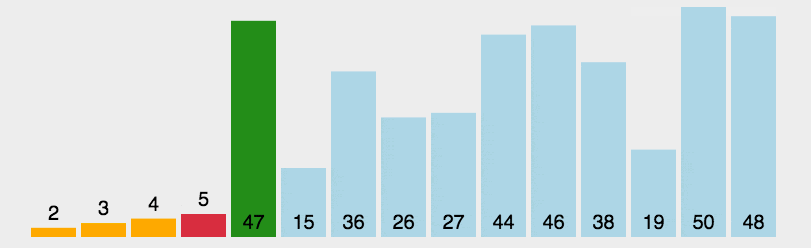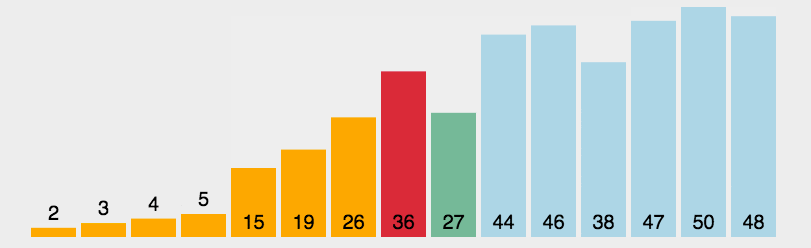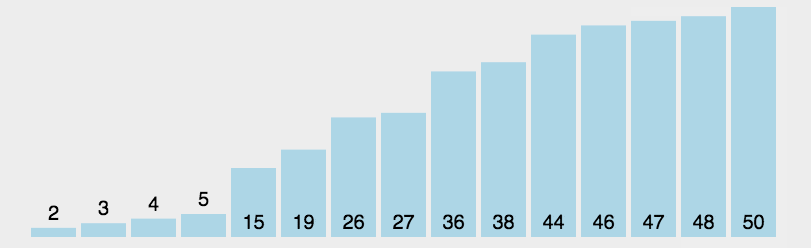
3. JavaScript 代码实现

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

4. Python 代码实现

def selectionSort(arr):
    for i in range(len(arr) - 1):
        # 记录最小数的索引
        minIndex = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[minIndex]:
                minIndex = j
        # i 不是最小数时，将 i 和最小数进行交换
        if i != minIndex:
            arr[i], arr[minIndex] = arr[minIndex], arr[i]
    return arr

5. Go 代码实现

func selectionSort(arr []int) []int {
    length := len(arr)
    for i := 0; i < length-1; i++ {
        min := i
        for j := i + 1; j < length; j++ {
            if arr[min] > arr[j] {
                min = j
            }
        }
        arr[i], arr[min] = arr[min], arr[i]
    }
    return arr
}

6. Java 代码实现

public class SelectionSort implements IArraySort {
    @Override
    public int[] sort(int[] sourceArray) throws Exception {
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        // 总共要经过 N-1 轮比较
        for (int i = 0; i < arr.length - 1; i++) {
            int min = i;
            // 每轮需要比较的次数 N-i
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    // 记录目前能找到的最小值元素的下标
                    min = j;
                }
            }
            // 将找到的最小值和i位置所在的值进行交换
            if (i != min) {
                int tmp = arr[i];
                arr[i] = arr[min];
                arr[min] = tmp;
            }
        }
        return arr;
    }
}